ГЛАВА V.
ЧТО ТАКОЕ ЛОГАРИФМ?
5. Логарифм как площадь.
В § 3 мы рассматривали движение по особому закону, и особая связь переменных, времени t = x и длины пути s = y, дала нам новую функцию —логарифм. В § 4 мы ввели специальное число, а именно — значение длины пути s при значении t=1, и обозначили эту длину через «е». Число е даёт возможность производить вычисления для отдельных изолированных значений х. Естественно поставить вопрос: нельзя ли найти формулу (рецепт), позволяющую быстро и легко по данному значению s найти соответствующее значение t?
Оказывается, это возможно: вся следующая глава будет посвящена выводу такой формулы (ключ Меркатора). Но в порядке подготовки к этому выводу, мы сначала должны дать совершенно другое истолкование той связи, той функциональной зависимости, которая существует между переменными величинами s и t.
В настоящем параграфе мы покажем, что если величину s представить в виде абсциссы, то величина t (т. е. логарифм) может быть представлена в виде некоторой криволинейной площади. На прилагаемом чертеже (черт. 52, а) ордината PN = у = s означает достигнутое движущейся точкой расстояние от начальной точки, абсцисса ОР = х = t - протекшее время. По некоторым соображениям, которые будут выяснены дальше, длину ординаты PN следует брать меньшей, чем 2 ед.; возьмём, например, ее равной 1,8 ед. Как найти соответствующее значение абсциссы t или х?
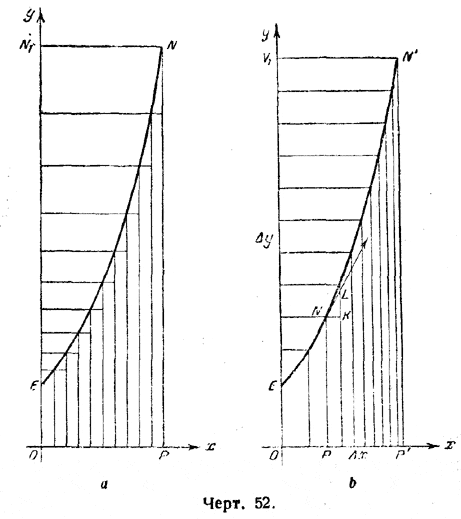
С этой целью разделим (черт. 52, b) длину пройденного пути от s = l до s =1,8 на равные доли и будем для каждой такой доли подсчитывать требуемый для её прохождения промежуток времени.
Для очень мелкого элемента пути s = y скорость можно приближённо считать постоянной и равной, например, расстоянию до начала этого элемента (или же до конца его). Если дистанция [1 ... 1,8] разделена, например, на 80 равных долей, то, считая на элементах пути [1...1,01]; [1,01 ... l,02]; [l,02... 1,03]; ... , [1,56... 1,57]; [1,57... 1,58]; ..., [1,79... 1,80] скорость соответственно равной 1 м/час; 1,01 м/час; 1,02 м/час.....1,56 м/час; 1,57 м/час.....1,79 м/час и постоянной на каждом элементе пути, найдём, что затраченные на их прохождение промежутки времени будут равны:
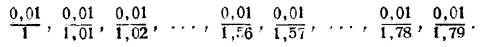
Сумма всех этих промежутков времени:
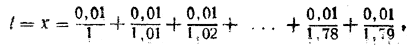
или в более общей записи:
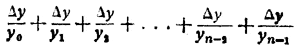
даёт приближённое значение всего интервала времени. Результат будет точнее, если разделить дистанцию [1 ... 1,8] на 800 равных долей, на 8000 равных долей и т. д. Чем больше число долей п, тем точнее результат. Рассматриваемые суммы принято записывать в виде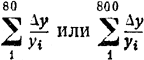 
и т. д. При нашем стремлении получить совершенно точное значение всего интервала времени t = x, мы должны неограниченно увеличивать число п долей. Таким образом, искомая величина представляется нам, как предел суммы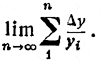 
Этот предел суммы получил в математике название интеграла и особое обозначение:
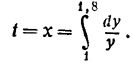
Для дальнейшего будет полезно сделать некоторое преобразование того графика движения Непера, который мы до сих пор рассматривали. Цель этого преобразования такова: так как мы по данной длине пути s отыскиваем время t, то будет удобнее, чтобы исходная величина s была откладываема по горизонтали, а искомая величина t — по вертикали.
Вообразим себе (черт. 53) зеркало, поставленное перпендикулярно к плоскости чертежа вдоль прямой ОН, биссектрисы координатного угла. Тогда, вычертив на том же чертеже зеркальное отражение первоначального графика, мы увидим, что каждой точке М прежнего графика будет отвечать некоторая точка М нового. Нетрудно видеть, что абсциссе точки М отвечает равная ей ордината точки М, и наоборот, т. е.
x = y , y = x
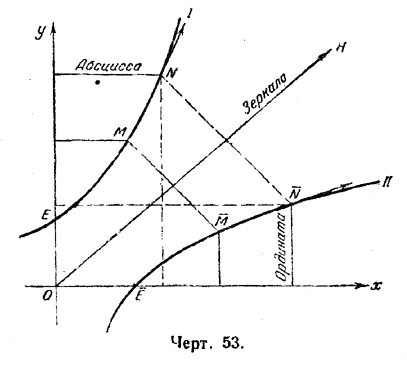
Каков будет закон построения новой кривой E N? Если для первой (I) кривой наклон её (т. е. тангенс угла касательной с горизонталью) был численно равен ординате у, то у новой кривой наклон будет иметь обратное значение: касательная ко второй (II) кривой симметрична с касательной к первой (I) относительно биссектрисы ОН. Если, например, в точке М имеем tg = 8/5 то в симметричной точке М имеем tg = 5/8 , так как
tg = tg (90° — ) = ctg = 1/tg .
И если для первой (I) кривой мы имеем закономерность tg = y, то для второй (II) кривой, казалось бы имеет место соотношение tg = 1/y. Но это неправильно: дело в том, что при отражении в зeркале «ордината» переходит в «абсциссу», а потому величину у в точке N следует заменить величиной х в точке N.
В результате, для любой точки N второй (II) кривой имеет место равенство:
угловой коэффициент касательной tg = 1/x.
После того как прежняя (I) кривая Непера была отражена в зеркале, мы имеем уже новую (II) кривую и в дальнейшем мы сосредоточим внимание именно на ней.
Она получила название логарифмической, так как для неё по горизонтали откладываются обычные числа (путь), а по вертикали логарифм (т. е. протекшее время).
Для дальнейших выводов будет целесообразно переменить роли «пути» и «времени». А именно, будем и новую кривую рассматривать как график движения другого типа (черт. 54) и, как обычно принято, считать, что вдоль горизонтальной оси откладывается протекшее время t, а вдоль вертикальной—длина пройденного пути s.
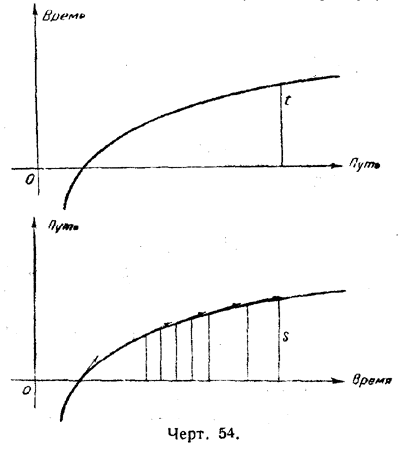
Только что выведенное свойство II кривой можно, отбрасывая чёрточки над буквами, записать так:
tg = 1/x.
Так как тангенс угла наклона касательной означает скорость, то движение нового типа можно характеризовать следующим образом.
Воображаемый путник в момент t = 1 (час) только выходит из начальной точки; путник всё время держит в руках часы; в начале каждой доли времени (например, каждой секунды) путник, посмотрев на часы (например, показывающие 1,2 часа), мгновенно находит обратное значение (например, 1/1,2) , т.е. вместо t берёт 1/t , и движется со скоростью v = 1/t в течение взятой доли времени. Весь подсчёт, рассмотренный нами выше, вида
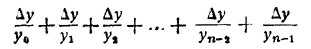
остаётся прежним, но теперь мы берём не приращения пути у, а приращения времени х, и не делим на скорость у, а умножаем на новую скорость v = 1/t . Поэтому получим новую сумму вида
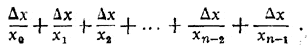
Для точного подсчёта нам попрежнему надо будет взять предел такой суммы, т. е. интеграл:
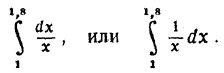
Выполним ещё одно—последнее геометрическое преобразование для искомой величины (т. е. логарифма). А именно, для последнего рассмотренного движения, когда переменная скорость в любой момент t численно равна обратному значению 1/t , построим график скоростей. Оставляя неизменной ось Ох = Ot, будем откладывать вдоль оси Оу не длину пути, а скорость. Читатель, вероятно, встречал такой график скорости в курсе физики (черт. 55). Тогда, в силу закона рассматриваемого движения, графиком скорости будет служить уже знакомая нам по предыдущим главам гипербола
y = v = 1/t = 1/x
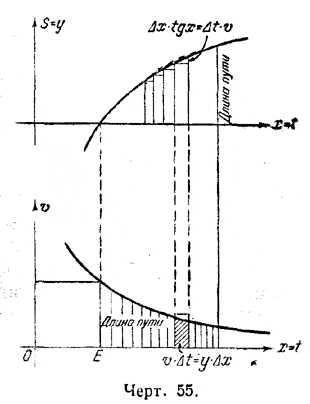
Элемент пути теперь представится в виде произведения ординаты 1/x на малое приращение абсциссы х = t, т. е. узким прямоугольником:
s = v • t = y • х = 1/x • х ( = площади узкого прямоугольника).
Совокупность площадей таких тонких, элементарных прямоугольников даст в пределе некоторую криволинейную площадь. Величина этой суммарной площади численно будет равна искомой длине пути, т. е. логарифму.
На черт. 55 одновременно показаны: на верхнем графике—элементы пути в виде приращений ординаты:
у = х • tg ,
на нижнем графике — те же элементы пути в виде узких прямоугольников. Правда, на верхнем чертеже элементы пути представлены отрезками, т. е. геометрической величиной первого измерения, а внизу — площадкой, т. е. величиной второго измерения, но численно те и другие величины постоянно остаются соответственно равными,
Мы имеем здесь различие геометрического изображения при одном и том же арифметическом содержании.
Но вторая форма более наглядна, более осязательна, она ближе нашему чувственному восприятию. Поэтому в последнее время некоторые учёные предложили, чтобы и в школе ученикам разъяснять логарифм наглядно в виде площади, а именно так:
Определение. Логарифмом некоторого числа z называется величина криволинейной площади, ограниченной сверху дугой гиперболы и взятой на интервале [1 ... z ]
Эта площадь замещает ординату у логарифмической кривой, о которой шла речь выше. И если раньше основное свойство, связывающее числа yiс их логарифмами xi, записывалось в виде:
при у1• у2 = у3 х1 + х2 = х3,
то теперь это же основное свойство примет следующую форму:
пл.[1 . . . z1] + пл. [1 ... z2] = пл. [1 ... z1 • z2].
Это —как раз то свойство площади, ограниченной дугой гиперболы и прямолинейными отрезками, о котором шла речь во II главе. Но если раньше это свойство геометрической модели логарифма появилось как бы неожиданно, случайно и было лишь слабо связано с понятием отношения двух чисел, то теперь оно представляется как звено в общей теории, оно вплетается в общую сеть закономерностей, причём в основе всей теории лежит идея Непера.
В заключение этой главы скажем несколько слов о привычном, «школьном» определении логарифма.
Мы видим ,что при неперовом движении log е = 1, log (е2) = 2, log (е3) = 3 и т. д. Если х — рациональное число, т. е. если он равняется дроби m/n, где m и п — целые числа,то и в этом случае log (ex) = x. Таким образом логарифм степени числа е равняется показателю степени, в которую возводится число е. В случае бригговых логарифмов вместо числа е приходится рассматривать степени числа 10.
Мы приходим к привычному определению логарифма:
логарифмом числа N по основанию а называется показатель степени, в которую нужно возвести а, чтобы получить N.
Это определение хорошо тем, что позволяет очень просто вывести все нужные формулы и быстро перейти к практическим вычислениям. В силу этих причин его кладут в основу школьного изложения теории логарифмов.
Но здесь нужно сделать важное замечание. При неперовом движении (движении непрерывном) время может принимать не только рациональные, но и иррациональные значения. Так, например, при t = 2 непременно найдётся соответствующее ему значение расстояния s (именно в силу непрерывности движения). В этом случае, как и в случае рационального значения t, пишут s = e t = e2 , получая совершенно естественно иррациональные степени числа е. Меняя масштаб неперовой кривой , можно столь же естественно получить степень с иррациональным показателем при любом основании а, например, при а = 10.
Мало того. Формула, данная в параграфе 4, которую можно записать так:
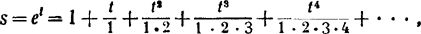
позволяет легко вычислить, с какой угодно степенью точности, любую степень числа е, независимо от того, рационален или иррационален её показатель.
Если же, как это делается обычно в школе, дать формальное определение логарифма, не обосновывая при этом учения об иррациональных показателях, то всё учение о логарифмах окажется построенным на песке.